Author Archives: Peter

Data Processing in SAS

Libraries
Libraries are directories where your datasets are stored. It is a good idea to declare a local library where you want store the dataset after you’re done processing it. They can be declared with the libname function. Here i declare the library out. Any datasets stored in this library can be accessed by preceding the dataset name with the library name, in library.dataset format. Read the data step section to see this in action.

libname out 'C:\sasdata';

Data Step
The data step is where new data is introduced into SAS, and one way to create new variables. SAS has many, many ways to move data into the program, and to manipulate it once it’s in place. We will only go into a few.

  • Cards – The first method available is to enter the data directly. Using the cards command in the data step, we can create the dataset without referencing outside files. 
    data out.projdata;
	input a b;
	cards;
	0 1
	1 2
	3 2
	4 1
	;
	run;

    Note that in this data step, I am creating the permanent dataset out.projdata, with 4 observations of 2 variables. On a side note, “cards” is a holdover from when punch cards were used to enter data. The command “datalines” can be used as well.

  • Set – Set allows us to call existing SAS datasets. Data stored on the machine in the sas format, .sas7bdat, can be called by name into SAS. Give the folder they reside in a library name, and reference them by name using the library.dataset format. 
    data out.projdata2;
	set out.projdata;
	c = a+b;
	run;
  • Infile – Infile allows us to reference an exterior file that’s not stored in SAS’s dataset format. There are many options to this, but in general datasets stored in .csv or .txt are relatively easy to import. There will be made reference to something called a delimiter. This is a character that separates data stored in 2 columns. For instance, if a row had 2,1,3,4, then the delimiter would be a comma. 
    data out.projdata;
        infile "C:\sasdata\data.txt" dlm= '|' firstobs=1;
        input a b c d;
        run;

    In this statement, we see that the file I’m reading in is using a pipe ‘|’ as the delimiter. In files that use tab delimiting, we have to use the hex representation of tab, ’09’x.

    data out.projdata;
        infile "C:\sasdata\data.txt" dlm='09'x firstobs=1;
        input a b c d;
        run;

    The file I’m importing in this datastep has 4 variables that I’m giving arbitrary names.

  • Proc Import – Not a data step, but another important way to get data into SAS is proc import. This gives us much more flexibility than the infile command in the datastep. 
    proc import datafile="C:\sasdata\data.txt";
        out=out.projdata;
        dbms=dlm;
        delimiter='|';
        run;

    This command is even easier if we are importing a .csv. In that case, the dbms option is csv, and the delimiter is assumed as a comma.

Multiple Linear Regression (SAS)

In this tutorial, we will be attempting linear regression and variable selection using the cirrhosis dataset. We attempt to predict incidence of cirrhosis on a population using a few descriptor variables from that population. The variables we have are:

  • urbanpop – The size of the urban population
  • lowbirth – the reciprocal of the number of births to women between 45 and 49, times 100
  • wine – Consumption of wine per capita
  • liquor – Consumption of hard liquor per capita
  • cirrhosis – The death rate from cirrhosis

First step in analysis is of course to read the data in to SAS. Download the dataset, and replace the filepath with what it is on your machine. (try shift-right-click on the drinking.txt file)

filename fn 'filepath\drinking.txt'; /* replace filepath to run code */
 
data liquor;           /* New dataset 'liquor' */
	infile fn;     /* using dataset at previously declared filepath */
	input id one urbanpop lowbirth wine liquor cirrhosis;
	run;           /* id and one are unnecessary */
 
data liquor;
        set liquor(drop=id one);  /* Dropping unnecessary variables */
        run;

Declaring a filename variable isn’t necessary, but does make the resulting code look better. The variable ID is a unique identifier for each observation, and isn’t really necessary. Similarly, the variable one is just a vector of ones. We can safely eliminate both. the next step is to begin preliminary data analysis. A good idea is to see how correlated the data is. To do this we try

proc corr data=liquor;
        var urbanpop lowbirth wine liquor;
	run;

We can see that the data is heavily correlated. As we are trying to avoid multicollinearity, we can expect that some of the predictors will be dropped from the model.

proc reg data=liquor;
	model cirrhosis = urbanpop lowbirth wine liquor;
	run;

The t values for both urbanpop and liquor are insignificant with the other 3 in the model. We have some other choices we can look at before doing variable selection. A good thing to look at is VIF, or Variance Inflation Factor. The higher the VIF, the more that variable can be predicted by the other variables in the model, and thus the higher the multicollinearity. The VIF gives an estimate of how much the variance of the coefficients is increased by the inclusion of that variable. We tend to try to keep the VIF for any particular variable under 5.

proc reg data=liquor;
	model cirrhosis = urbanpop lowbirth wine liquor/vif covb;
	run;

The VIF for lowbirth is the highest, so we might consider removing that variable from the model. However, urbanpop also has a high VIF, and is not significant in the model. It would be a good idea to remove that variable from the model before continuing. Because I’m also going to demonstrate variable selection via stepwise, I’m going to leave it in.

The covb option gives the variance/covariance matrix of the beta coefficients. It allows you to determine how closely related any two covariates are. This method is not quite as useful as VIF, because it only checks for pairwise correlation, whereas VIF checks for true multicollinearity. However, it is a good idea to look at this matrix to understand your data better.

proc reg data=liquor;
	model cirrhosis = urbanpop lowbirth wine liquor/p r influence;
	run;

The P option gives the predicted values for each observation. The R option gives each observations residuals, along with a graphic method of viewing those residuals. This provides another way of finding outliers.

The influence option gives us the ability to see how much influence any given observation had on the overall fit, or any of the beta values. Variables with Cook’s Distance greater than .10 are generally termed as outliers. In keeping with the principles of linear regression, we don’t want any individual points having too much influence on the fit of a regression, or the individual beta’s.

proc reg data=liquor;
	model cirrhosis = urbanpop lowbirth wine liquor/selection=stepwise;
	run;

Here we finally try running stepwise variable selection. The criteria used is AIC, or Akaike’s Information Criterion. A model that has a lower AIC is considered better. In doing variable selection, SAS removes both urbanpop and liquor from the model, confirming our earlier assessment that they were not helpful in fitting the model. In looking at the R^2 value, The value did not change much, however the adjusted R^2 is slightly better. Of course, this does not really showcase the value of stepwise variable selection as it tells us what we already knew.

proc reg data=liquor;
	model cirrhosis = lowbirth wine/p cli clm;
	run;

This is our final model. As we already went over, p gives the predicted value for each observation. cli gives the prediction interval for that observation (interpret as in what interval would a new observation with those covariates fall into?), while clm gives the confidence interval for that observation (interpret as in what interval would a bunch of new observations with those covariates fall under?).

Simple Linear Regression (SAS)

In this tutorial we will conduct simple linear regression on a dataset on an example dataset. In the dataset there are 62 individuals, and we will be regressing brain weight over body weight. As stated before, in simple linear regression we are trying to find a linear relationship between the dependent and independent variable, that can be modeled as

    \begin{equation*} Y_i = \beta_0 + \beta_1X_i + \err_i \hspace{2cm} \err_i \sim N(0,\sigma^2) \end{equation*}

The dataset we will be using today was pulled from a set of example datasets, linked in the sample data section. I have hosted it at this website here, so you must download the dataset to follow along. This regression will attempt to find a linear relationship between body weight, and brain weight.

FILENAME FN 'filepath\brainbody.txt';

This step isn’t really necessary, but I did want to demonstrate the ability to create filename variables to simplify subsequent proc statements.

DATA BB;              /* creating a dataset named BB         */
     INFILE FN;       /* Input File fn (declared previously) */
     INPUT INDEX BRAINWEIGHT BODYWEIGHT;/* Variables in file */
     RUN;             /* run the datastep                    */
 
DATA BB;                   /* Create a new dataset BB        */
     SET BB(DROP=INDEX);   /* Using existing set (sans index)*/
     RUN;                  /* run the datastep               */

The reason I drop the index variable is because it is unnecessary. Due to our using simple infile statements, we have to read all the data in and then drop the data we don’t need. There are more advanced input statments you could use that don’t have that limitation, but for such a small dataset this is the easiest option. Now to build a model, we use the proc reg statment.

PROC REG DATA=BB;  /*  Regression on BB Dataset             */
     MODEL BRAINWEIGHT = BODYWEIGHT; /* Brain ~ Body        */
     RUN;          /*  Run the Regression                   */

fit1By default, the proc reg statement generates quite a bit of output. The individual t statistics test significance of point estimates for slope and intercept, while the F statistic is the overall significance of the regression. They say that the regression is significant, so that there is a linear effect. However, none of these statistics accurately capture what is wrong with this fit. Look at the diagnostic plots, the fitted vs residual plots, and the QQ plot. They warn of something very wrong here. In the “Quantile to Quantile” (or QQ) plot, we see how closesly the residuals from the fit match a normal distribution. They don’t. Given that one of the assumptions of least squares linear regression is that the residuals follow a normal distribution, we can see we have a problem here. We can also see this by the histogram of residuals on the bottom, with a superimposed normal curve. It is clear to see that the residuals do not follow a normal distribution. To fix this, one thing we can do to make a valid model is to attempt transformations of the variables. A reasonable choice might be a log transform of the independent variable.

DATA BB;            /* Create new Dataset BB                */
     SET BB;        /* Using existing Set BB                */
     LOGBODYWEIGHT = LOG(BODYWEIGHT);
                    /* Add log transform of Bodyweight      */
     RUN;
 
PROC REG DATA=BB;   /* Run the Regression again on new BB   */
     MODEL BRAINWEIGHT = LOGBODYWEIGHT;
                    /* Brain weight Versus log(bodyweight)  */
     RUN;

fit2We attempt a log transformation of the independent variable to remove some of the skew. In looking at the F statistic and the t-statistics for the individual \beta‘s, we can see that the regression is still significant. However, the transformation actually makes the fit significantly worse. We see a clear pattern in the residuals, and a QQ plot that appears almost flat where it should be diagonal. Considering that log transforming the dependent variable without transforming the independent variable would just skew the data the other way, another choice we have would be to log transform both independent and dependent variables.

DATA BB;             /* Create new Data-set BB              */
     SET BB;         /* Using existing set BB               */
     LOGBRAINWEIGHT = LOG(BRAINWEIGHT);
                     /* Log Transform of Brain Weight       */
     RUN;
 
PROC REG DATA=BB;   /* Create new Regression Model using BB */
     MODEL LOGBRAINWEIGHT = LOGBODYWEIGHT;
                    /* Log(Brainweight) ~ Log(BodyWeight)   */
     RUN;

fit3We attempt a log transform of both the independent and dependent variables. Here we can see the data nicely nested around the fitted line. This is ideally the plot we’re looking for in simple linear regression. We see a strong correllation and an interpretable relationship. Observing the diagnostic plots we see no obvious patterns in the fitted vs residual plot, and the QQ plot follows the diagonal fairly well.fit3plot It diverges a bit towards the tails, so there may be a slightly better transformation we could apply, but we can regard this fit as “good enough”.

On the fit plot, we see the 95% confidence limits, and the 95% prediction limits. This will require some explanation. Confidence Intervals refer to confidence in the parameter of the generating function. IE, we are 95% confident that the parameter that generated that data falls within that interval. They are generated as a function of the coefficient’s value and standard deviation.

Prediction limits on the other hand add in the extra variability of the error term to say that we are 95% sure that any new observation will fall within the bounds. See the theory page for the math required to generate the confidence and prediction intervals.

Now for some math. Taking the log of both sides is in effect performing exponential regression. When we solve the revised equation for the original y, we get this.

    \begin{align*} \ln(y) &= -2.51 + 1.225\ln(x) + \err\\ e^{\ln(y)} &= e^{-2.51 + 1.225\ln(x) + \err}\\ y &= e^{-2.51}e^{\ln(x)^{1.225}}e^{\err}\\ y &= e^{-2.51 + \err}x^{1.225} \end{align*}

And this is the final relationship we arrive at with this data set.

Further Reading

Tutorial Papers Library (SAS)

Spatial/Spatio-Temporal Statistics

Logistic Regression

Logistic Regression is a method of classification using the regression framework. In logistic regression, the output (or target, or dependent) variable y_i is a binary variable, taking values of either 0,1. The predictor (or input, or independent) variables x_{i,j} are not limited in this way, and can take any value.

Logistic regression is based on the logistic function, which always takes values between 0 and 1. Replacing the dependent variable of the logistic function with a linear combination of dependent variables we intend to use for regression, we arrive at the formula for logistic regression.

    \begin{equation*} \pi(X_i) = \frac{1}{1+ e^{-(\beta'X_i)}} \hspace{1cm} \beta'X_i = \beta_0 + \beta_1x_{i,1} + \beta_2x_{i,2} + \ldots + \beta_px_{i,p} \end{equation*}

Where X_i is the vector of independent variable observations for subject i with a preceding 1 to match \beta_0. \beta is the vector of coefficients. We can interpret \pi(x) as the probability p(y_i=1|X_i). I.e., the probability that the dependent variable is of class 1, given the independent variables.

To get an idea of what’s happening here, we’re going to introduce an idea called “odds”. Odds are a ratio of probabilities. Let’s say P is the probability of an event occuring. 1-P is the probability of that event not occuring. Odds is defined as \frac{P}{1-P}. IE, the ratio of probabilities of that event occuring over that event not occuring.

The Logit function is given

    \begin{equation*} \logit(p) = \log(\frac{P}{1-P}) \end{equation*}

or, the log-odds ratio. The logit function has the interesting property that \logit(1-p) = -\logit(p). So now, we declare the logit equal to the linear combination of covariates.

    \begin{equation*} \logit(\pi(x)) = \beta'X \hspace{1cm}\Rightarrow\hspace{1cm}\pi(x) = \frac{1}{1+e^{-(\beta'X)}} \end{equation*}

But now we’re solving for the \logit(\pi(x)). We can solve this using the least squared error solution from linear regression.

    \begin{align*} \logit(\pi(X)) &= X\beta\\ X'Y &= X'X\beta\\ \beta &= (X'X)^{-1}X'Y \end{align*}

This solves for the \beta that minimizes the squared error. We should specify that in Logistic Regression, the errors are assumed to be binomial.

Logistic Regression (R)

Logistic Regression is a type of classification model. In classification models, we attempt to predict the outcome of categorical dependent variables, using one or more independent variables. The independent variables can be either categorical or numerical.

Logistic regression is based on the logistic function, which always takes values between 0 and 1. Replacing the dependent variable of the logistic function with a linear combination of dependent variables we intend to use for regression, we arrive at the formula for logistic regression.

    \begin{equation*} \pi(x) = \frac{1}{1+ e^{-(\beta'X)}} \hspace{1cm} \beta'X = \beta_0 + \beta_1x_1 + \beta_2x_2 + \ldots \end{equation*}

We can interpret \pi(x) as the probability p(y=1|X). I.e., the probability that the dependent variable is of class 1, given the independent variables.

For this tutorial, we will be performing logistic regression on the “Adult” dataset. I have previously explained the data preparation and transformations that I use for this dataset in this tutorial. We can import the dataset and repeat the transformations using the provided source file.

source("https://scg.sdsu.edu/wp-content/uploads/2013/09/dataprep.r")

To fit the logistic regression model, we will use the glm method. This is available in vanilla R without any other packages necessary. However, some packages provide more options for model fitting and model diagnostics than is available here. I also recommend the rms package, as it contains natively many different diagnostic tests for all sorts of regression.

fit1 = glm(income ~ ., family = binomial(logit), data = data$train)

Here for the formula, I am fitting income versus all other variables in the data frame. glm expects a family, which asks for the family of the error function, and the type of link function. Here I’m using Binomial errors, and the link function is logit, for logistic regression.

fit1sw = step(fit1)  # Keeps all variables

the step() function iteratively tries to remove predictor variables from the model in an attempt to delete variables that do not significantly add to the fit. The stepwise model selection schema was covered in the regression schema tutorial. It is unchanged in this application.

It is interesting to note here that by AIC, the stepwise model selection schema kept all variables in the model. We will want to choose another criteria to check the variables included. A good choice is the variable inflation factor.

The variable inflation factor in the car package provides a useful means of checking multicollinearity. Multicollinearity is what happens when a given predictor in the model can be approximated by a linear combination of the other predictors in the model. This means that your inputs to the model are not independent of each other. This has the effect of increasing the variance of model coefficients. We want to decrease the variance to make our models more significant, more robust. That’s why it’s a good idea to omit variables from the model which exhibit a high degree of multicollinearity.

The VIF for a given predictor variable can be calculated by taking a linear regression of that predictor variable on all other predictor variables in the model. From that fit, we can pull an R^2 value. The VIF is then calculated as

    \begin{equation*} VIF_{i} = \frac{1}{1-R_i^2} \end{equation*}

where VIF is the variable inflation factor for variable i, R_i^2 is the Coefficient of Determination for a model where the ith variable is fit against all other predictor variables in the model. In this case, because we’re using logistic regression, the car package implements a slightly different VIF calculation called GVIF, or generalized VIF. The interpretation is similar. On normal VIF in multiple regression, we attempt to eliminate variables with a VIF higher than 5.

library(car)
vif(fit1)

We see from the output of the VIF function, that the variables marital, and relationship are heavily collinear. We will eliminate one of them from the model. I will choose relationship, as its meaning is somewhat difficult to understand, and thus limits our ability to interpret the model. We will now fit the new model using the glm() function.

fit2 = glm(income ~.-relationship, family = binomial(logit), 
       data = data$train)
vif(fit2)

VIF for fit2 finds no variables with a high VIF. Therefore the model passes the multicollinearity test. There are a few other tests we can give the model before declaring it valid. The first is the Durbin Watson test, which tests for correlated residuals (An assumption we make is for non-correllated residuals). We can also try the crPlots() function. It plots the residuals against the predictors, allowing us to see which categorical variables contributed the most to variance, or allowing us to spot possible patterns in the residuals on numerical variables.

durbinWatsonTest(fit2)
crPlots(fit2)

With a Durbin Watson statistic of 1.975, an associated p-value of .096, we fail to reject the null hypothesis, that the errors are correllated. We can call the model valid. But we do have one more means of testing the overall fit of the model, and that is empirical justification. We will see how well the model predicts on new data. In the dataprep() function called in the source(…) line, we split the complete dataset into 2 parts: the training dataset, and the validation dataset. We will now predict based on the validation dataset, and use those predictions to build a ROC curve to assess the performance of our model.

library(ROCR)
fitpreds = predict(fit2,newdata=data$val,type="response")
fitpred = prediction(fitpreds,data$val$income)
fitperf = performance(fitpred,"tpr","fpr")
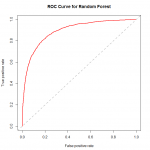
plot(fitperf,col="green",lwd=2,main="ROC Curve for Logistic:  Adult")
abline(a=0,b=1,lwd=2,lty=2,col="gray")

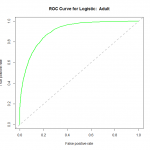ROC Curve for Logistic Regression on Adult DatasetWe can see that the performance of the model rises well above the diagonal line, indicating we are doing much better than random guess. As to how well this particular model fares against other models, we would need to compare their ROC curves using the same datasets for training and validation.

Bagging

Ensemble methods combine multiple classifiers into a single output. Some ensemble methods may combine different types of classifiers, but the ones we will focus on here combine multiple iterations of the same type of classifier. These methods belong to a family of ensemble methods called “Perturb and Combine”.

Perturb and Combine

Some methods of classification are extremely sensitive to noise in the data. In these, small changes in the data can have huge impacts on the model itself. We call these unstable models. However, the instability does not hugely affect the accuracy of the model.

Perturb and Combine models attempt to take advantage of this instability by iteratively perturbing the data and training a new classifier. At the end, we combine the models together by voting. Some perturbation methods include

  • Resampling – Taking additional samples from a population
  • Subsampling – Taking samples from the original dataset
  • Adding Noise – Adding noise to the original dataset
  • Adaptively Reweight – This is for the Boosting Algorithm

Perturb and Combine methods attempt to train the model to signal in the data, and drown out the noise. For that purpose, we perturb the data and train models, then combine the trained classifiers. The idea is that while every model will be wrong to some extent, by using models with high variance we hope they will be wrong in different ways. In this way, by averaging we will get a model that is reliably better than any individual model. This guide will focus on Bagging, which falls under the Subsampling Method.

Bagging

Bagging stands for Bootstrap Aggregation. Bootstrapping is a method of iteratively subsampling the data. For a given dataset, we draw a sample of size t \leq n with replacement from the original dataset. The goal is that iteratively drawing from the existing sample, we can simulate new draws from the population. Aggregation refers to aggregating the class votes from the models trained on each of the bootstrap samples.

  • For i in 1 to B (the number of bootstrap samples)
    • Take a bootstrap sample of size t\leq n: X* =(X_1*,\ldots,X_t*)
    • Train a model on X*
  • Now you have a set of trained classifiers to make predictions with. The final aggregate classifier can be obtained by averaging the output probabilities.

Notes for Use

Bagging reduces Variance. Each single classifier is unstable, meaning it has high variance. The aggregated classifier reduces the variance, without increasing the bias. (assuming we’re using a low bias model.) Bagging works well for unstable learning algorithms. However, bagging can actually slightly degrade the performance of stable learning agorithms, so it’s only appropriate on models with low bias and high variance. A good example meeting these criteria are tree based models, as we’ll see.

Random Forest

The Random Forest method is an extension of bagging when applied to tree models. Random Forest attempts to increase the variance of individual tree models, with the hope of capturing more information about the data. In Random Forest, we attempt to increase the variance of the individual models in 2 ways:

  • We introduce the m_{try} concept. At each split, rather than trying every possible split on every variable, we randomly select m_{try} variables from the set and attempt to make a split on one of those variables
  • We do not prune the individual models. We leave them in their fully grown state

Random Forests can be implemented in R using the randomForest package.

Random Forests (R)

We will apply the random forest method to the Adult dataset here.

We will begin by importing the data, doing some pre-filtering and combining into classes, and generating two subsets of the data: The training set, which we will be using to train the random Forest model, and the evaluation set, which we will use to evaluate the performance of the model.

source("https://scg.sdsu.edu/wp-content/uploads/2013/09/dataprep.r")

For more information on what this source code does to prepare the data, visit the tutorial: “Data Preparation with R (Adult Dataset)”. This allows us to move on to model specification.

Random Forests are an extension of tree methods. Where in the CART methodology, the inherent variability of the tree model, and susceptibility to data was considered a weakness of the model, in random forest that is considered a strength. In fact, we take special steps to ensure as much variability in the individual trees as possible. The belief is that by averaging across the high variance, low bias trees, we will end up with a low bias, low variance estimator. We hope that the random forest will do better than any single tree could do. We need to load up the libraries we’ll be using.

library(randomForest)
library(ROCR)

Next we’ll need to find the optimal numbers of variables to try splitting on at each node.

bestmtry <- tuneRF(data$train[-13],data$train$income, ntreeTry=100, 
     stepFactor=1.5,improve=0.01, trace=TRUE, plot=TRUE, dobest=FALSE)

For this, the syntax I’m using for the tuneRF function means I’m giving the function the first 12 columns of the training set (all values but income) as independent variables. The specification data$train[-13] means “All but the 13th column on the set data$train”. As an independent variable, I give the algorithm “data$train$income”, which is the income column on the set data$train. ntreeTry specifies the number of trees to make using this function, trying out different numbers for mtry. See the help file (help(tunerf)) for more information.

The algorithm has chosen 2 as the optimal number of mtry for each tree. Now what we have left to do is run the algorithm.

adult.rf <-randomForest(income~.,data=data$train, mtry=2, ntree=1000, 
     keep.forest=TRUE, importance=TRUE,test=data$val)

In the formula for Random Forest, we specify income versus all other variables in the set as predictors. We specify the mtry value to be 2, matching what we had found earlier with searching for the optimal value. The number of trees we use here is 1000, though computers are fast now and it’s not unreasonable to use 20,000 or more trees to build the model. We ask the algorithm to keep the forest, as well as calculate the variable importance so we can see what contributed most to estimating income classification.

Finally, we can evaluate the performance of the random forest for classification. Since we have been eschewing the confusion matrix in favor of the ROC curve, we should probably continue that. The commands to generate the ROC curve using the ROCR package are as follows:

adult.rf.pr = predict(adult.rf,type="prob",newdata=data$val)[,2]
adult.rf.pred = prediction(adult.rf.pr, data$val$income)
adult.rf.perf = performance(adult.rf.pred,"tpr","fpr")
plot(adult.rf.perf,main="ROC Curve for Random Forest",col=2,lwd=2)
abline(a=0,b=1,lwd=2,lty=2,col="gray")

adult_rf_rocTo build the ROC curve using the ROCR package, first we need to generate the prediction object. As inputs to the prediction() method, we use the predicted class probabilities for the validation dataset, and the actual classes (labels). There are various things we can do with the prediction object, but the most appropriate here is to gauge the performance, using the performance() method. As inputs, we give it the performance object, and the two metrics we want to display in the ROC curve. (True positive rate, False positive rate). There are other diagnostic curves we can also generate using this method. See help(performance) for more information.

To interpret the ROC curve, let us remember that perfect classification happens at 100% True positive rate, and 0% False positive rate. With that in mind, we see that perfect classification happens at the upper left-hand corner of the graph, so the closer our graph comes to that corner, the better we are at classification. The diagonal line represents random guess, so the distance of our graph over the diagonal line represents how much better we are doing than random guess. Now we also want to evaluate what variables were most important in generating the forest.

importance(adult.rf)
varImpPlot(adult.rf)

Variable Importance (Random Forest)The importance() function gives us a textual representation of how important the variables were in classifying income, while the varImpPlot() method gives us a graphical representation. We see from the Variable importance plot, that the most important variables included age, capital gains, education, and marital and relationship status. Variables like race and country of origin were of less importance.

Classification Trees (R)

Classification trees are non-parametric methods to recursively partition the data into more “pure” nodes, based on splitting rules. See the guide on classification trees in the theory section for more information. Here, we’ll be using the rpart package in R to accomplish the classification task on the Adult dataset. We’ll begin by loading the dataset and library we’ll be using to build the model.

source("https://scg.sdsu.edu/wp-content/uploads/2013/09/dataprep.r")
library(rpart)

The name of the library rpart stands for Recursive Partitioning. The source(“…/dataprep.r”) line runs the code located at that URL. For information in what is contained in that code, check the R tutorial on the Adult dataset. The code prepares and splits the data for further analysis.

mycontrol = rpart.control(cp = 0, xval = 10)
fittree = rpart(income~., method = "class",
     data = data$train, control = mycontrol)
fittree$cptable

If we observe the fitted tree’s CP table (Matrix of Information on optimal prunings given Complexity Parameter), we can observe the best tree. We look for the tree with the highest cross-validated error less than the minimum cross-validated error plus the standard deviation of the error at that tree. In this case, we observe the minimum cross-validated error to be 0.6214039, happening at tree 16 (with 62 splits). There we observe the standard error of that cross-validated error to be 0.01004344. We add these values together to get our maximum target error. We find the CP value for the tree with the largest cross-validated error less than 0.6314473. This occurs at tree 8, with 11 splits.

cptarg = sqrt(fittree$cptable[7,1]*fittree$cptable[8,1])
prunedtree = prune(fittree,cp=cptarg)

Plot of Classification TreeWe then prune with tree 8 as our target tree. To ensure we get tree 8, the CP value we give to the pruning algorithm is the geometric midpoint of CP values for tree 8 and tree 7.We can plot the tree in R using the plot command, but it’s a bit of work to get a good looking output.

par(mfrow = c(1, 1), mar = c(1, 1, 1, 1))
plot(prunedtree, uniform = T, compress = T, 
     margin = 0.1, branch = 0.3)
text(prunedtree, use.n = T, digits = 3, cex = 0.6)

We can now move to evaluating the fit. First we can generate the confusion matrix.

fit.preds = predict(prunedtree,newdata=data$val,type="class")
fit.table = table(data$val$income,fit.preds)
fit.table

Another way to check the output of the classifier is with a ROC (Receiver Operating Characteristics) Curve. This plots the true positive rate against the false positive rate, and gives us a visual feedback as to how well our model is performing. The package we will use for this is ROCR.

library(ROCR)
fit.pr = predict(prunedtree,newdata=data$val,type="prob")[,2]
fit.pred = prediction(fit.pr,data$val$income)
fit.perf = performance(fit.pred,"tpr","fpr")
plot(fit.perf,lwd=2,col="blue",
     main="ROC:  Classification Trees on Adult Dataset")
abline(a=0,b=1)

Receiver Operating Characteristics for RpartOrdinarily, using the confusion matrix for creating the ROC curve would give us a single point (as it is based off True positive rate vs false positive rate). What we do here is ask the prediction algorithm to give class probabilities to each observation, and then we plot the performance of the prediction using class probability as a cutoff. This gives us the “smooth” ROC curve.

The full predict.rpart output from the model is a 2-column matrix containing class probabilities for both 0 (less than 50k) and 1 (greater than 50k) for each of the observations in the supplied dataset. Because the prediction() function expects simply the class probability of income being greater than 50k (IE, P(data$val$income == 1|model)), we need to supply only the second column.

R – Functions

Functions are methods of isolating tasks so that they can be repetitively applied. They follow a basic structure.

name = function(inputs in function scope){  # function declaration
  
  body # Here, There be Dragons!
  
  return(output)  # spits back the output
}

 # sometime later

name(inputs in global scope)  # function call

The Name of the function is the unique identifier of that function. Within R, we can create functions named whatever we want

Inputs are variables passed into a function. We can pass any number of variables we want. We can set default values for variables passed so that if we run a function repetitively with one of the inputs not changing, we can set that input to have a default value and not mention it in the function call.

When outside variables are passed into the function, they are assigned in-function scope variable names. Then within the function, these variables are manipulated without affecting the variables outside the function.

The return statement allows us to pass a variable back out from the function. This variable can be any type of data structure we may need. Now let’s look at a simple function.’

hw = function(){
  return("Hello World!")
}

a = hw()  # call the function, pass the output into new variable a
print(a)  # Print a

Now, we can write a slightly more advanced function to use input variables and perform manipulation on them.

bitstrings = function(n){ # declare bitstrings with the input n
  return(2^n)             # returns value of 2 to the n
}

print(bitstrings(8)) # prints the results of the call with n = 8

Because n = 8, we get a result of 256. There are 256 possible unique bitstrings when using 8 bits.

Functions are very useful if we want to only work on a subset of a given dataset at a time. We can use bracket notation to subset the dataset on a given variable (or set of variables), and then pass only that subset to the function for further analysis. I will expand more on this in the bracket notation section.

A good example of a function will be the body mass index Function. We pass it numeric inputs of height (in inches) and weight (in pounds). It follows the standard formula for BMI, and returns the value.

BMI = function(height,weight){
  return(0.45455*weight/(.0254*height)^2)
}
BMI(71,180)

Because the contents of the R-function can be done on 1 line without declaring any temporary variables, we can choose to omit the return() statement and define the function on one line. The following code is equivalent to the previous code.

BMI = function(height,weight){(0.45455*weight/(.0254*height)^2)}

This returns 25.1765, the BMI for a person who is 71 inches tall and weighs 180 lbs.

If we were so inclined, we could use some properties of more advanced data structures. Let us say we have the height and weight of several people. We can add another column to the data frame using the function.

h = c(68,70,65,74,69)
w = c(185,162,122,224,154)
people = data.frame(h,w)
people$bmi = BMI(people$h,people$w)
print(people)

So we can run multiple lines through custom functions without iterating between the lines.